Spectral Risk Measure

What is a Spectral Risk Measure?

Spectral risk measures are a complex subset of distortion risk measures that incorporate the investor’s risk tolerance level. It will give a larger weighting to bigger losses to try and better quantify an investors approach to risk.

They allow assigning different weightings across the distribution of potential losses, essentially the larger the potential loss the larger the weighting. While the distortion function transforms the cumulative distribution function of losses, the spectral function further refines that to reflect how much importance is given to each percentile of loss.

Spectral function must adhere to specific mathematical properties in requiring that the distortion function arise from a non-negative, increasing, and integrable (meaning the total “weight” of the spectrum is finite) weighting function. Unlike Value at Risk (VaR), which is a distortion risk measure (but not spectral) that only focuses on a fixed quantile, Conditional Value at Risk (CVaR) is a spectral risk measure that offers greater flexibility in applying constant weight to tail losses

Spectral Risk Measure Explained

Spectral risk measures offer a flexible and theoretically robust approach to quantifying financial risk. They are particularly useful for financial institutions and investors that require understanding and managing tail risk. Examples include pension funds, insurance companies, quantitative asset managers and/or central banks.

Although spectral risk measures are part of the wider classification of distortion risk measures, their specific feature is incorporating the investor’s risk preferences directly into the calculation. The way this is done is through a weighting function that emphasizes different parts of the loss distribution based on how risk-averse the user/investor is instead of treating all possible losses equally (or focusing only on a single percentile like VaR does). Such an approach provides a much better perspective of the overall downside risk and is especially useful during periods of market turbulence.

At their core, spectral risk measures are designed to evaluate the expected loss across all quantiles of a distribution. By using a spectral function, they apply a varying degree of emphasis to different parts of the loss spectrum, unlike simple averages or VaR. Usually, more weight is given to larger losses (i.e. higher percentiles), allowing the measure to reflect aversion to tail risk.

The below formula expresses the general form of a spectral risk:

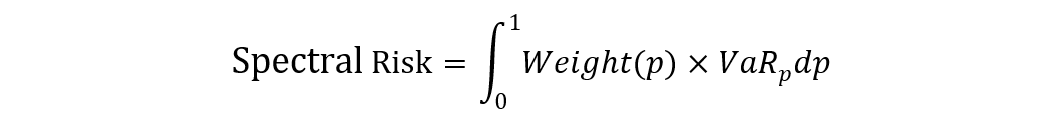
Where:

p = the probability level (from 0 to 1)

VaRp = the Value at Risk at level p

Weight(p) = how much emphasis is placed on losses at each level of p

As we noted above, to ensure the measure is coherent, the weight function must be:

• Non-negative
• Increasing
• Add up to 1 across all percentiles

Strategies Using Spectral Risk Measures

Strategies that consider sensitivity to tail risk or a specific level of risk aversion often use spectral risk measures. They enable portfolio managers to go beyond the mean-variance optimization by incorporating custom weightings that emphasize extreme losses.

In addition, they are also used to design portfolios that are stable under market stress scenarios. This is especially applicable to hedge funds, insurance portfolios and/or credit-sensitive strategies. For example, tail-hedging strategies typically adopt spectral risk constraints to dynamically scale exposures, adding more weight to assets with more favourable loss profiles. Portfolios invested in alternative assets would often use spectral measures to ensure that capital is not overly concentrated in instruments that contribute disproportionately to tail risk.

Example Using Spectral Risk Measures

In this example, we provide a real-world case scenario of how spectral risk measures could be used and interpreted.  Access the free Financial Edge template to download these scenarios and calculations.

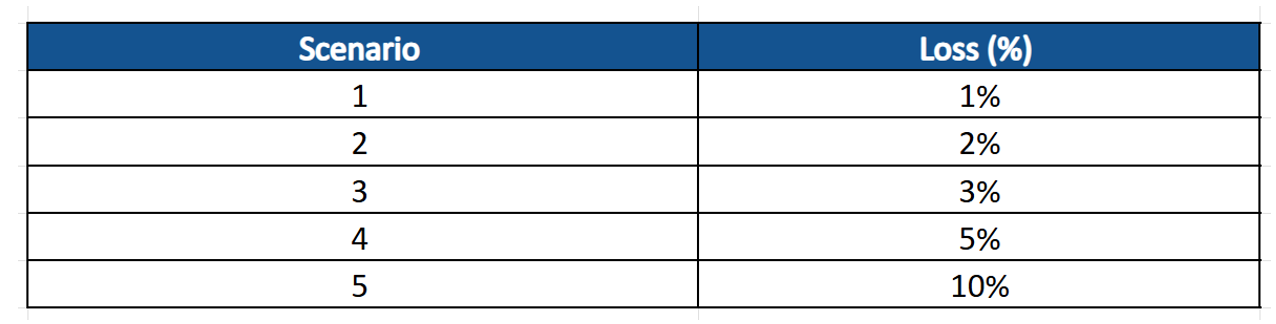
An equity portfolio manager has calculated the probability of a loss in five equally probable scenarios. These are shown in the table below:

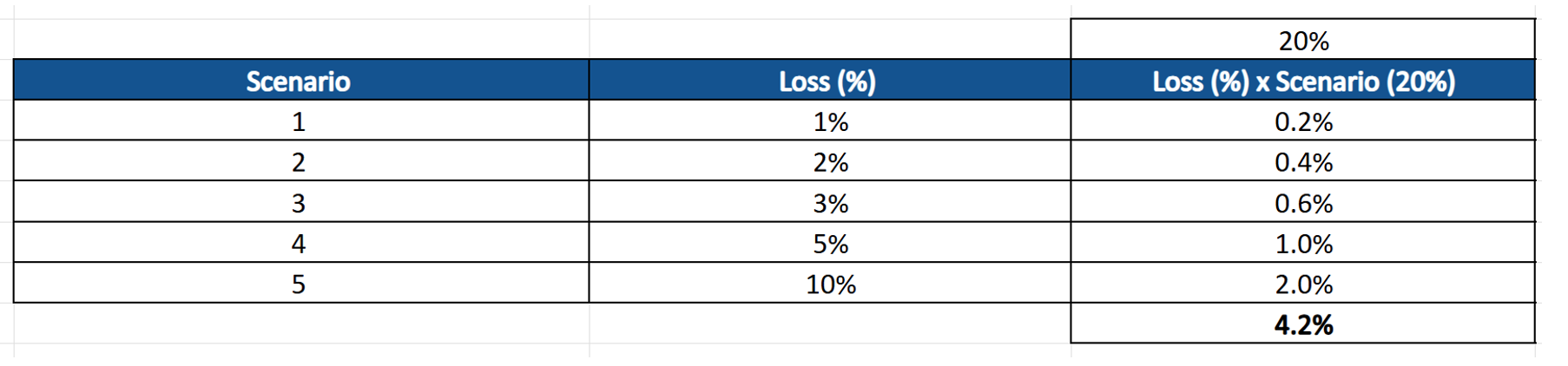
First, we can calculate the chance of each scenario generating a loss using a simple average method rather than any risk aversion method. Given we are told each of the five scenarios are equally likely, this equates to a 20% chance per scenario of a loss being generated.

We can then use this to calculate the expected loss from the scenarios:

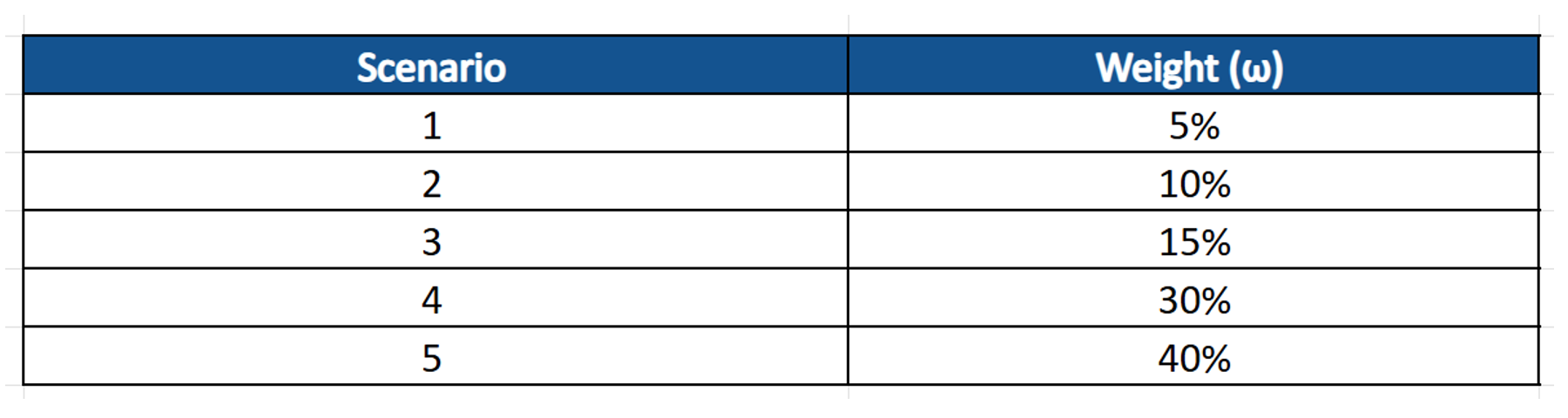
The portfolio manager has then applied a risk-averse spectral weight function that will place more emphasis on the scenarios which may generate higher losses. These weightings all add up to 1 – with Scenario 1 given the lowest weighting.

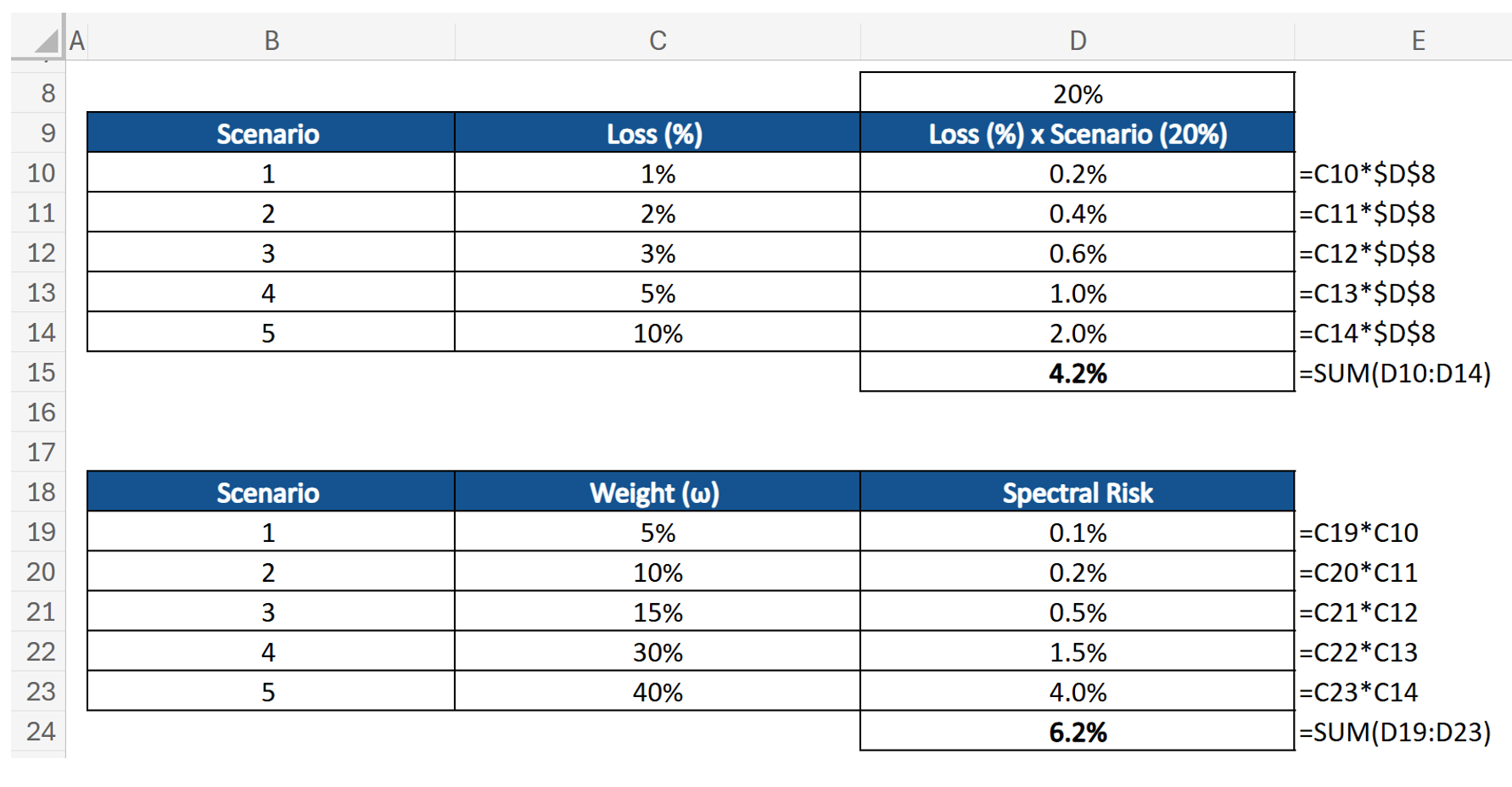
We can then calculate the spectral risk by taking the weighted average of the losses:

This shows that despite the average potential loss across all scenarios being 4.2%, the spectral risk is higher at 6.2%. This reflects a more conservative stance by overweighting tail events.

Applications

Spectral risk measures are getting increasingly popular in areas where sensitivity to tail events is critical. For example, portfolios invested in high yield bonds could be exposed to very rare but severe events. Through the customizable weighting feature of these measures, investors can fine-tune how cautious or aggressive their risk model should be.

Other examples include:

• Aligning capital reserves with worst-case obligations – pension funds and insurers use them for their asset-liability management
• Hedge funds and quantitative investors use them to optimize exposure to rare but impactful events such as volatility spikes or liquidity crunches
• Regulatory bodies and banking institutions use spectral risk measures to evaluate capital adequacy and solvency under stress scenarios

Limitations of Spectral Risk Measures

Although spectral risk measures offer a structured and flexible approach to risk assessment, they also have some limitations

• Subjective: choosing the spectral (weighting) function is rather subjective can be a key challenge
• Dependent on inputs: the final result can vary significantly depending on the investor’s input as different weight functions reflect different attitudes toward risk – making consistency and comparability across different investors very difficult
• Complex: The level of computational complexity could be of concern, especially for large or complex portfolios – where the quality and reliability of data is relatively weak in more niche asset classes
• Multi-Risk factors add more complexity: should the investor need to incorporate multiple risk factors that will add further complexity and the calculation would require more resource.
• Data Sensitivity: spectral risk measures can be highly reactive to small changes or noise in the extreme ends of the distribution (particularly in illiquid markets), which in turn could lead to overly conservative estimates

Conclusion

Spectral risk measures provide a refined approach to risk assessment. Although they are more complex to model, their deeper insights into potential losses are highly valued across risk-aware investors. Unlike more traditional metrics such as VaR, they are more coherent and account for the full distribution of losses, emphasizing those in the tail.

Spectral risk measures find many applications in areas such as portfolio construction, trading and regulatory compliance, where understanding extreme downside scenarios is key. Portfolio managers across different industries such as hedge funds, insurers and asset management, typically use spectral risk measures to limit their potential drawdowns and align risk exposures with their investment and fiduciary objectives.

Additional Resources

Liquid vs Illiquid Assets

Value at Risk

Portfolio Management Certification