Risk Premium
June 28, 2021
What is “Risk Premium”?
“Risk Premium” or “Market Risk Premium,” is the rate of return on an investment in excess or over and above the risk-free rate, for example, the US 364-day treasury bill that an investor seeks due to investing in high-risk investments, such as corporate bonds or stocks. Therefore, the “risk premium” represents the additional return that is above the risk-free rate. The higher (or lower) the market or asset class volatility, the higher (or lower) will be the (market) risk premium.
In the context of “risk premium”, it is important to know that the investment process involves the construction of an overall portfolio of assets – consisting of risky assets (stocks, corporate bonds etc) and risk-free assets and deciding how much capital to allocate between the risky portfolio and risk-free assets. Investors tend to desire an asset allocation that gives them the best or optimum risk return trade-off.
Key Learning Points
- In order to fully comprehend the concept of “Risk Premium,” it is imperative to understand the CAPM equation or formula
- The “Beta,” of a portfolio measures the systematic risk (i.e. market risks that cannot be diversified) and the sensitivity of a portfolio or security relative to changes in the market
- In essence, the CAPM equation states that the expected return on the overall portfolio is equal to the risk-free rate of return + the market risk premium, predicated on the beta of that portfolio
- The CAPM model is used to calculate the expected return
- Three main factors drive or influence the “Risk Premium” and they are: macroeconomic volatility, political risk and market structure
- The risk premium tends to be lower in developed markets and higher in emerging markets
Risk Premium
The “Capital Asset Pricing Model” (CAPM) provides us with a precise forecast of the relationship that we should observe between the risk of an asset and its expected return. In this model, there is a term known as “Risk Premium” or “Market Risk Premium,” which is the excess return on the risky portfolio (i.e. market portfolio) over and above the risk-free rate.
In order to apply the CAPM and therefore gain an insight to the risk premium, given below is the equation for this model:
E(Rp) = Rf + Bp * (E(Rm) – Rf)
The term E(Rp) refers to the expected return on the overall portfolio. Rf refers to the risk-free rate, Bp refers to what is known as “Beta” of a portfolio, which measures the systematic risk (i.e. market risks that cannot be diversified) and the sensitivity of a portfolio relative to changes in the market (i.e. beta is a measure of portfolio risk), E(Rm) refers to the expected rate of return on the market portfolio and the term (E(Rm) – Rf) refers to risk premium.
The term Bp * (E(Rm) – Rf) refers to the return on a portfolio which can be attributed to both the risk premium and beta.
In essence, this equation states that the expected return on the overall portfolio is equal to the risk free rate of return + the market risk premium, predicated on the beta of that portfolio.
There are factors that drive or influence the risk premium and the main ones that seem to influence the same are macroeconomic volatility, political risk and market structure.
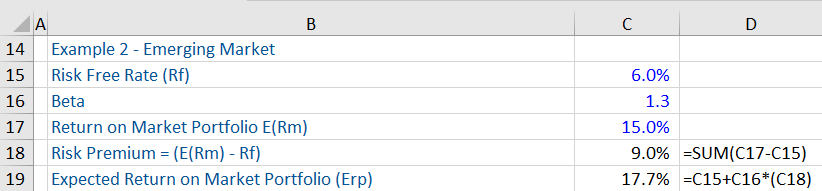
Risk Premium, Expected Return on Overall Portfolio and CAPM
Given below is a workout of the Risk Premium, calculated as: Market Risk Premium (E(Rm – Rf) and Expected Return on Overall Portfolio (Erp). In the first example, the risk premium is lower, as it’s a developed market, in this case, the US.
In the second example, the market risk premium is higher, as emerging markets tend to have higher market risk premium due to the aforesaid (3) factors.
From the two examples, one will gather that the higher (or lower) the risk premium, the higher (or lower) is the expected return on the market portfolio.
The risk premium over the government bond rate (i.e. risk-free rate) tends to be much higher in emerging markets than in developed markets.
While gaining an insight to risk premium and expected return on overall portfolio, one should know that when the beta coefficient is greater (less) than 1, it means that an asset (i.e., security or portfolio) carries greater systematic risk and volatility than the market (for example, S&P 500). So when the market rises, the asset rises by a greater percentage amount than the overall market.