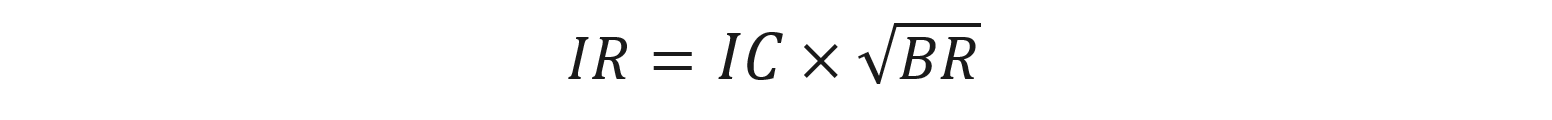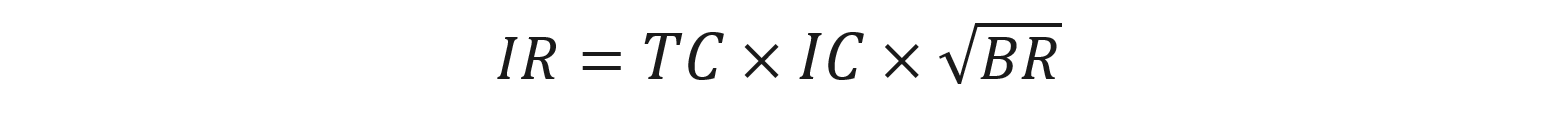Fundamental Law of Active Management

What is the Fundamental Law of Active Management?

The Fundamental Law of Active Management is a quantitative framework that links the capabilities of an active manager to generate excess returns to the skill and breadth of their investment decisions. It is formally expressed through the Information Ratio and aims to illustrate that returns are not only driven by accuracy but also by the number of uncorrelated bets taken by the manager.

Essentially, it suggests that consistent alpha generation is driven by both better insights and greater diversification of active positions. However, its practical application is often constrained by a number of factors such as correlated opportunities, estimation error and/or transaction costs.

The Basic Law (Unconstrained Portfolio)

The basic unconstrained form of the Fundamental Law of Active Management assumes that a portfolio manager can take any position independently of any benchmark restrictions. In this case, the calculation that explores the relationship between skill, opportunity and performance is:

Where:

IR = Information Ratio, which measures the efficiency of active returns
IC = Information Coefficient, which quantifies the forecasting skill
BR = Breadth, i.e. the number of independent decisions made for the period

The formula suggests that if each active bet adds incremental value (and each one is statistically independent), the overall performance scales with the square root of breadth.

This in theory means that a manager can sustain outperformance indefinitely by expanding the number of independent opportunities should forecasting skill remain constant. The basic version of the law is typically used as guidance/a benchmark for evaluating the best possible achievable returns. However, that ideal relationship begins to erode when practical considerations such as correlations or portfolio constraints are also added.

The Full Law (Constrained Portfolio)

The constrained version of the law expands the basic model to also account for the real-world challenges that portfolio managers face. These include constraints around positioning relative to a benchmark, risk budgets, turnover limits or liquidity restrictions. This would typically reduce a manager’s ability to fully reflect their own views in the portfolio.

To measure the efficiency with which forecasts are translated into active portfolio positions, the full law introduces the Transfer Coefficient (TC). This measure aims to tell how much of the manager’s good ideas actually make it in their portfolio. Good forecasts are not enough on their own as during the portfolio construction process managers usually face various constraints such as position sizing, liquidity or transaction costs. Essentially, these limitations can dilute the original forecasts.

From a technical perspective, the value of the Transfer Coefficient ranges between 0 and 1 and estimates the friction between excess return forecasts and the practical limitations imposed on portfolio construction. TC = 1 represents the unconstrained case, whereas a lower reading reflects tighter constraints or inefficient portfolio implementation. By capturing the degree to which the signal is diluted during implementation, the TC serves as a measure of implementation efficiency, quantifying the alignment of portfolio weights with the optimal active bets implied by forecasts. Within the context of the full law, the TC scales the achievable Information Ratio, where even high forecasting skill and ample breadth, a low TC suppresses realized performance. Therefore, maximizing the TC is critical to preserving alpha generation potential.

This full version of the law demonstrates that even with high forecasting skill and abundant breadth, actual returns are ultimately constrained by how effectively the manager’s insights can be expressed within the investment process. Therefore, managers typically optimize their portfolio construction approach in order to maximize the Transfer Coefficient and preserve their alpha generation potential.

Example: The Full Fundamental Law

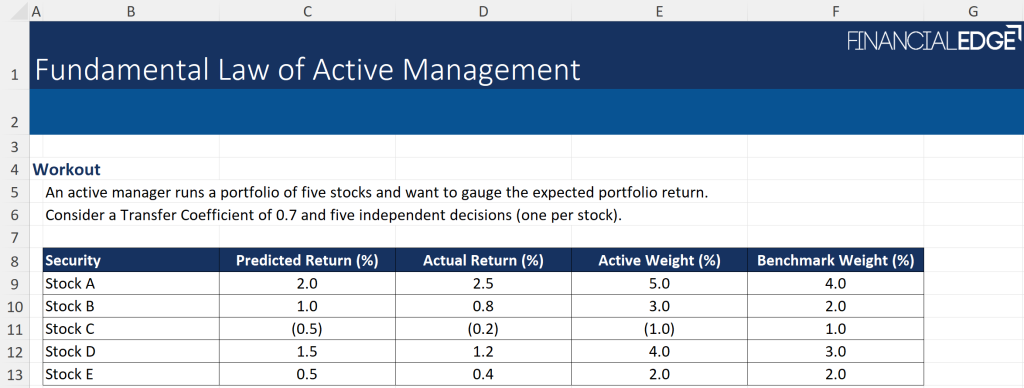
Below we provide a practical example of the full version (constrained portfolio) of the fundamental law. You can download the Excel files for free at the top of this page.

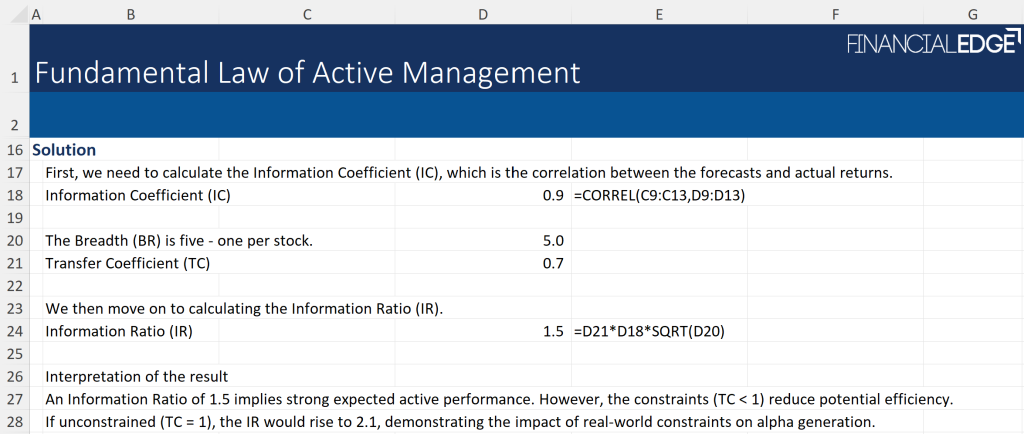
To calculate the Information Ratio, we need to first find out what the Information Coefficient (IC) is.

The Transfer Coefficient (TC) and the Breadth (BR) are provided.

The final calculation and the interpretation of the result are shown below.

Ex-Post Performance Measurement

Ex-post performance measurement evaluates the actual returns achieved by an active manager against the performance implied by their forecasted skill, opportunity set and implementation efficiency. Although the law is typically expressed in ex-ante (forward-looking) terms, the ex-post calculation examines the relationship between the IC, BR and TC using past data (i.e. after the fact).

This requires calculating the:

• The realized Information Ratio: defined by the average realized alpha divided by its tracking error.
• The ex-post Information Coefficient: estimated as the correlation between predicted and realized returns over time, reflecting actual forecasting effectiveness.
• The ex-post Transfer Coefficient: inferred by comparing realized active positions to the unconstrained optimal ones implied by the forecasts.

The aim of this process is to provide insights into the components of realized performance, skill, breadth and implementation efficiency. For example, a decline in ex-post Information Ratio against ex-ante expectations could indicate a highly constrained portfolio, insufficient independent positions or overestimation of skill. Therefore, quantifying these elements transforms the law into a practical tool for evaluating and validating active investment processes.

Zero-Sum Game and Alpha Generation

The concept of a “zero-sum game” states that for every unit of outperformance achieved by one investor there is an equivalent underperformance by others (before costs). It is key in understanding the sources of alpha generation and further evidences the competitive nature of active management. Producing excess returns (against a benchmark or the average market participant) requires skill, knowledge and execution efficiency relative to peers, not just achieving positive returns in isolation.

As the market is “zero-sum”, generating alpha is not just a function of identifying profitable opportunities, but also of exploiting them more effectively than competitors. The more independent bets a manager can make and the more accurately forecasts predict outcomes, the greater the potential Information Ratio, even within the “zero-sum” environment. However, it is essential to note that transaction costs, market impact and fees turn the theoretical “zero-sum game” into a negative-sum environment, which makes skillful alpha generation even more important.

Conclusion

The Fundamental Law of Active Management helps investors understand the drivers of active investment performance. It quantifies how skill and opportunity translate into alpha with its unconstrained form exploring the theoretical potential of skill and breadth and the constrained version looking into the limitations imposed by portfolio constraints. The law also emphasizes the “zero-sum” nature of active management, in which outperformance is achieved relative to other market participants.