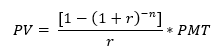Annuity
What is an Annuity?
An annuity is a regular payment made every year for a finite period. An example of an annuity is regular interest payments received from investing in a 10-year bond. Another example of an annuity is monthly payments made on mortgages. They are common for retirement planning purposes. Annuities help calculate how much one should invest today to get a fixed payment every year after a certain number of years.
Key Learning Points
- An annuity is a series of payments made at regular intervals for a finite period
- Annuities are common in pension planning and long-term debt products e.g. mortgages
- Three variables are needed to calculate the present of an annuity: interest rate (r), payment (PMT), and number of periods (n)
- The payment amount and time periods must be consistent, for example, if PMT is a yearly payment then n must be in years
- Excel has a present value function which can be used to simplify the PV calculation
Calculating the Present Value of an Annuity
Here is the formula for calculating the present value of an annuity:
PV Annuity Formula
Where
PV = Present value
PMT = Yearly payment
r = Interest rate
n = Number of years
Annuities Explained
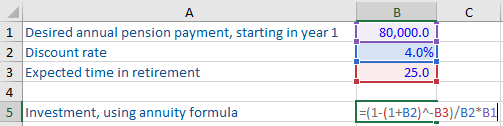
Let us understand with an example. Suppose you estimate you will have 25 years in retirement. Starting from year 1 of your retirement, you desire an annual pension payment of 80,000. You plan to invest in a relatively safe investment, so you are comfortable with a low discount rate of 4%. For the interest of simplicity, we shall assume this interest rate is fixed and ignore the impact of inflation. How much should you invest at the start of the retirement period?
Using the annuity formula in Excel, we get the investment amount as follows:
As per the formula, you need to invest 1,249,766 or roughly 1.25 million now in order to get an income of 80,000 every year for the following 25 years.
Excel has its own function to calculate the present value of an investment shown below:
Excel function = PV(rate, nper, pmt, [fv], [type])
Entering the numbers into the formulas returns the same answer.
Growing Annuity Value
In the real world, you also need to account for inflation. If you get a fixed amount every year, it may not be enough to keep up with increasing prices. That is where a growing annuity is used. A growing annuity is where the amount in annual payments received grows every year at a certain percentage.
The formula for the present value of a growing annuity is as follows:
Where
PV = Present value
PMT = Yearly payment
r = Interest rate
n = Number of years
g = Growth rate
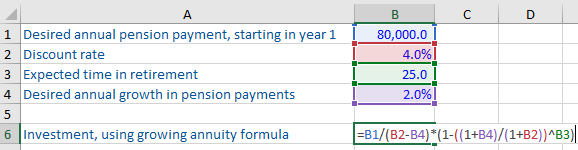
Let us calculate a growing annuity using the same values as in the previous example. The only addition is that the annual income of 80,000 will grow every year at a rate of 2%.
As you can see, if you want your pension payments of 80,000 per year to grow at 2% annually, you need to invest a higher amount (roughly 1.5 million) at the start of the retirement period.
Future Value of an Ordinary Annuity
Annuities can also be used to determine the future value of a series of payments to be made. For example, before taking a loan on interest, it will be good to calculate how much the loan is going to cost you.
Let us say you are borrowing 4,500 for 5 years at an interest rate of 6%. As per the terms of repayment, you are required to pay off 1,000 every year for the next 5 years plus any residual balance at the end. How much will you pay in total?
The formula for calculating the future value of an annuity is:
The calculation of the future value of an ordinary annuity would look as follows:
As you can see, you will end up paying 5,637 over a period of 5 years for your loan of 4,500. This formula helps borrowers in comparing multiple repayment options. For example, you may want to negotiate either the interest rate or the annual payment to reduce the total amount payable.
Excel has another function to calculate the future value of an investment shown below:
Excel function = FV(rate, nper, pmt, [PV], [type])
Using the numbers in the function returns the same value.