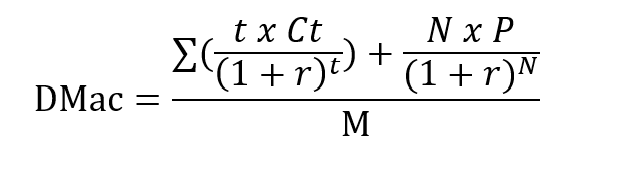Sign up to access your free download and get new article notifications, exclusive offers and more.
Duration Template
Bond Duration
June 3, 2025
What is Bond Duration?
Bond duration is a key measure of risk in fixed income portfolio management. It estimates the bond’s sensitivity to interest rate changes, i.e. how much its price will change in response to a change in interest rates. The higher the duration, the more sensitive the bond is to interest rate changes, meaning its price will be more volatile. Conversely, shorter durations indicate lower risk. There are two main types of duration – the Macaulay Duration and Modified Duration (which estimates price change for a 1% interest rate change).
Key Learning Points
- Duration is a measure of the sensitivity of a bond to changes in interest rates and it is based on the inverse relationship between interest rates and bond prices (when interest rates rise, the price of bonds falls and vice versa)
- It is a linear approximation for small changes in yield and assumes that duration stays the same along the yield curve (which is often not the case). Therefore, it is less accurate for larger changes in interest rates.
- The two main types of duration are Macaulay duration and Modified duration. Effective duration is also a popular variation, which accounts for flexible payments and follows a more complex calculation model
- Institutional investors such as pension funds, insurers and asset managers would typically use a specific duration strategy to help achieve their goals such as meeting future obligations (through using immunisation)
How Duration Works in Investing?
In investing, duration is used to gauge bond’s price sensitivity to changes in interest rates (i.e. the level of risk) as mentioned above. To illustrate that, below is a chart that shows how duration works in practice.
Generally, longer maturity means more time for interest rates to change and affect the bond’s price, respectively. The higher sensitivity of longer-dated bonds is due to time value of money or the discounting of future cash flows. As a result, longer-dated bonds with low coupons should have longer durations, whereas those with shorter maturities and/or higher coupons would have shorter durations and their prices are less sensitive to interest rate changes. Longer-dated bonds that have a low coupon rate will generate a larger proportion of its cash flows in the later years of the bond’s term making it more sensitive to rate changes
Types of Duration
Macaulay Duration
The Macaulay duration, sometimes also referred to as “Pure” duration, is named after the Canadian economist Frederick Macaulay, who first introduced the metric to bond income investing. It is designed to help investors assess the time aspect of cash flow recovery by showing how long it would take for the initial price paid for the bond to be recovered through a combination of both interest payments and capital repayment. A higher reading would indicate a longer time to recover the initial price paid, which in turn lead to higher sensitivity (more risk), and vice versa.
Modified Duration
The modified duration is another key variant in fixed income investing, which also measures the sensitivity of a bond’s price to changes in interest rates. It is based on the concept that interest rates and bond prices have an inverse relationship and estimates the percentage impact that a 100-basis-point (or 1%) change in interest rates will have on the bond’s price. Unlike the Macaulay duration, which focuses on the time aspect of cash flow recovery, modified duration focuses on the percentage change in the value of a bond and is directly used in risk management and bond pricing.
Effective Duration vs. Modified Duration
The effective duration is another important metric in analysing the sensitivity of a bond’s price to changes in interest rates, but it is however applied to different portfolios. It is used for bonds that have embedded options and takes into account that expected cash flows will vary as interest rates change.
For example, callable bonds allow the issuer to “call” the bond (repaying the principal to the bondholder earlier) before its maturity date. This may occur in a falling rates environment where issuers are able to call bonds with higher coupons and reissue debt at lower rates. This is where the effective duration helps investors to assess the expected cash flows from the bond by calculating the volatility of interest rates in relation to the yield curve. It estimates the expected decline of a bond’s price when interest rates rise by 1% and its value should always be lower than the maturity of the bond.
Below is a table that summarises the key differences between the effective and the modified duration.
| Modified Duration | Effective Duration | |
| Purpose | Measures price sensitivity assuming fixed cash flows | Measures price sensitivity allowing for variable cash flows |
| Application | Vanilla Bonds (with no embedded options or other forms of variable payments) | Bonds with embedded options, for example callable or putable |
| Cash Flows Assumption | Fixed and unchanged | Variable and interest rate–sensitive |
| Based On | Yield to maturity | Interest rate model |
| Calculation | Formula-based (relatively straightforward) | Model-based (more complex) |
| Example | Treasury bonds | Callable municipal bonds or mortgage-backed securities (MBS) |
Portfolio Duration Formula
The portfolio duration formula can be expressed according to the two main types of duration – the Macaulay and the modified duration.
DMac=(∑((t x Ct)/(1+r)^t )+(N x P)/〖(1+r)〗^N )/M
Where:
t = Time period (years) of each cash flow
Ct = Coupon payment in period t
r = Yield to maturity (YTM) per period
N = Total number of periods (maturity)
P = Present value (price) of the bond
M (Face Value) = Principal repayment at maturity
Modified Duration Formula
Modified Duration= DMac/((1+YTM/n))
Where:
DMac = the time it would take for an investor to recover the money initially invested in the bond
YTM = Yield to Maturity, which measures the total return on a bond if held until maturity
n = the number of coupon periods per year
DURATION Function
DURATION is a financial function in Microsoft Excel that calculates the duration of a bond that pays interest on a periodic basis. It can be found under financial functions and effectively calculates the Macaulay Duration.
Formula
=DURATION(settlement, maturity, coupon, yield, frequency, [basis])
Components:
- Settlement date
- Maturity date
- Coupon rate
- Annual yield
- Annual number of coupon payments
In the below example, we calculate the duration of a coupon purchased on the 1st of July 2020, with a maturity date of 30th of June 2030, and a coupon rate of 4%. The yield is 3% and payments are made biannually.
You may notice that there is an optional component at the end of the formula called “basis”. This is related to the type of day count basis to be used and is an optional input.
Solution
Strategies for Using Duration
Duration is used across several bond strategies, some of which we outline below:
- Immunisation – it is often used by pension funds or insurance companies to meet future obligations by matching the duration of assets and liabilities in order to protect against changes in interest rates
- Yield Curve strategies
- Active Duration Management – it involves shifting duration based on interest rate forecasts:
- If the investor expects rate cuts, duration is extended
- If rate hikes are expected, then duration is shortened
- Using Derivatives – some complex approaches may use derivatives to control duration. Using interest rate futures, swaps, or options to quickly adjust a portfolio’s duration without trading physical bonds, provides lower transaction costs and higher flexibility
Conclusion
To sum up, bond duration is a fundamental measure of the bond’s price sensitivity to changes in interest rates and is crucial in managing fixed income risk. It provides investors with an estimate of how much a bond’s price will change when interest rates rise or fall and is useful for aligning investment strategies with interest rate expectations. Short-duration bonds usually offer lower risk but also lower return potential, while long-duration bonds are more volatile but can offer higher returns (more specifically, in a declining rates environment).