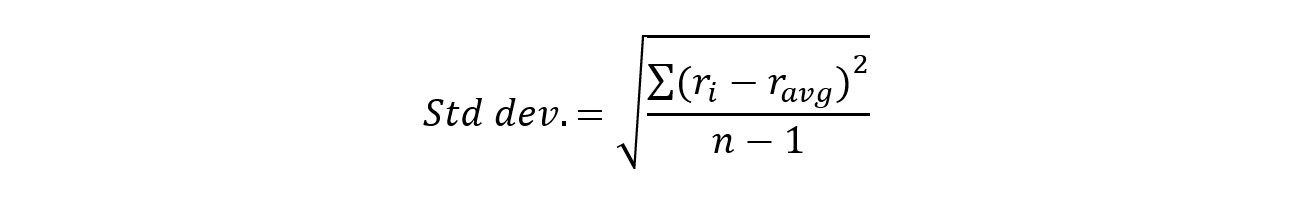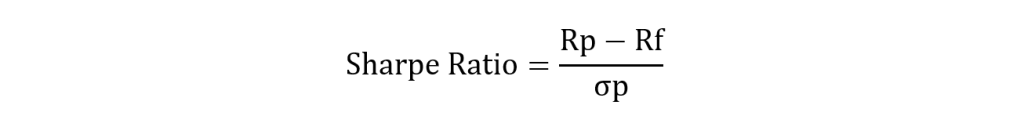Deviation Risk Measure

What is a Deviation Risk Measure?

Deviation risk measures are risk assessment tools that investors use to calculate the degree to which investment returns vary from its average over time. Unlike measures that purely focus on the magnitude of the potential loss like Value at Risk (VaR), this type of measures accounts for both down and upside moves and provide a perspective of the overall volatility.

Standard deviation is the most popular deviation risk metric and shows how widely returns can vary from the mean. Other examples include the downside deviation measure that offers a perspective on the downside by focusing only on negative returns.

Investors who focus on capital preservation or have a moderate risk appetite would typically find these measures useful. They often seek investments that are consistently stable or show a specific volatility range. In addition, in cases when returns are not evenly distributed, deviation risk measures could be quite helpful. They also feature in the calculation of popular risk-adjusted performance metrics like the Sharpe ratio, which makes them a practical alternative to traditional risk models.

Deviation Risk Measure Explained

Deviation risk measures aim to quantify the deviation of returns from a central tendency, for example the mean or median. They account for the overall dispersion of returns and therefore offer a wider perspective on volatility, unlike purely downside-focused measures.

Investors usually look into these measures because they reflect both the likelihood of losses and the unpredictability of gains.

Example of Deviation Risk Measure

A fund that invests in blue chip US companies has delivered 1% average monthly over the past year. However, during some months it delivered over 5%, while others posted more than 3% loss.

The standard deviation of returns for the fund is 4%, which indicates that over the period performance often deviated by 4% from the average. In practice, this quantifies the uncertainty that the underlying investors in the fund face each month, since returns could range between -3% and +5% around the average.

If a competitor fund shows the same 1% mean return but with lower deviation, for example 2%, some investors may prefer it as the outcomes are supposed to be more predictable.

Benefits of Deviation Risk Measure

There are several practical benefits that deviation risk measures provide. Let’s look into the most important ones below:

• They are particularly useful in financial risk management and quantify the deviation of an asset’s returns from its expected average
• Deviation risk measures can also guide asset allocation and support portfolio managers in perceiving the best possible risk-return asset mix
• These measures are also relatively straightforward to calculate and interpret (unlike spectral risk measures) which makes them broadly applicable across different portfolios and asset classes
• They also help investors to assess downside potential by isolating negative return deviations (downside risk)
  • This helps managers with capital preservation objectives or stricter risk constrains

Limitations of Deviation Risk Measure

On the other hand, investors should also bear in mind some limitations such as:

• Standard deviation accounts for both positive and negative volatility equally (i.e. treating them symmetrically), which can misrepresent risk and lead to overly conservative portfolio allocations
• Deviation measures can overlook fat-tailed distributions and leave portfolios exposed to tail risk (i.e. rare but severe events that are relevant during periods of market stress)
• They ignore the order of returns, which is often important for cash flow-sensitive investments such as mutual funds.
  • For example, a portfolio that suffers early losses may be riskier than a similar alternative with the same deviation but a different return path
• Deviation metrics do not directly consider macroeconomic or liquidity risks, which in turn could lead to underestimation of the real-world/market exposure

What is Standard Deviation?

Standard deviation is a statistical measure that quantifies the amount of variation in a set of values. Investors such as asset managers and hedge funds typically use it to assess the volatility of returns of an asset, portfolio holdings or the portfolio as a whole. A higher reading indicates greater variability and higher risk respectively, while a lower value suggests more stable returns and lower risk.

For example, if an equity portfolio stock has a standard deviation of 10%, its returns typically fluctuate 10% above or below the average. Investors can use it to evaluate the consistency of returns and also to compare the risk levels of different portfolios (or individual investments).

Calculating Standard Deviation

Standard deviation is calculated as the square root of variance by examining the variation between each data point (in this case the price of an asset) against the average. This is represented in the below formula.

Std dev.= √ (∑ (r_i-r_avg) ^ 2 / (n-1))

Where:

ri= return observed in one period

rvag = the average i.e. the arithmetic mean of the returns within the dataset

n = the number of observations in the dataset

Deviation Risk Example

Download the free Financial Edge excel Deviation Risk measure template.

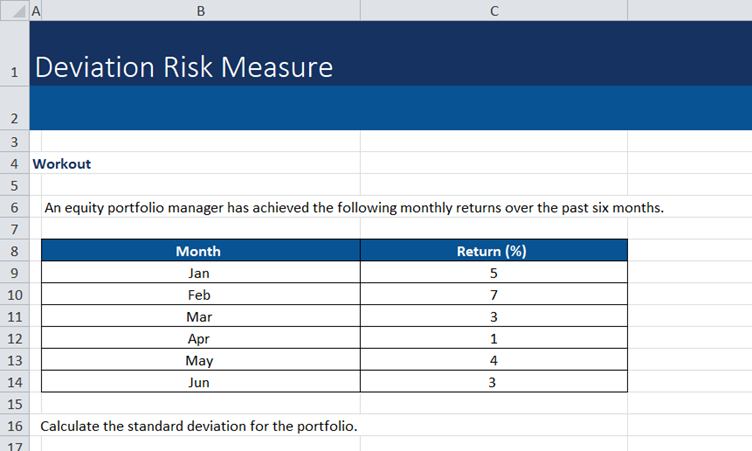
These are the steps to follow when calculating standard deviation:

1. Calculate the mean (average) return from the six months of data provided

Mean = (5+7+3+1+4+3) / 6 = 3.8

2. Find deviations from the mean

– 3.8) = 1.2; (7 – 3.8) = 3.2; (3 – 3.8) = -0.8; (1 – 3.8) = -2.8; (4 – 3.8) = 0.2; (3 – 3.8) = -0.8

• Square the deviations

1.4, 10, 0.7, 8, 0, 0.7

• Average squared deviations (variance)

Variance=  (1.4+10+0.7+8+0+0.7)/6=3.5

• Take the square root (standard deviation)

σ=√3.5=1.9

The standard deviation of returns is 1.9%, meaning returns typically deviate by about 1.9 percentage points from the average.

Limitations of Using Standard Deviation

Despite that standard deviation is widely used to measure volatility and assess investment risk, it also has several limitations that we list below:

• It assumes a normal distribution of returns, which in reality isn’t always the case as returns can be skewed or exhibit fat tails. This can result in the underestimation of tail risks
• In addition, it treats all deviations from the mean equally (whether gains or losses) while investors are typically more concerned about downside risk
• Standard deviation could be heavily influenced by outliers or short-term volatility, which in turn could distort the true risk profile of a long-term investment
• It offers no insight into the direction of volatility or its causes
• For complex portfolios that invest in instruments like derivatives, standard deviation may not fully capture the embedded risks

How are Standard Deviation and Variance Related?

Standard deviation and variance are closely related and both are used to assess risk through the dispersion of data points (i.e. returns). Variance measures how far each data point in a set is from the mean, on average, but does so by squaring the differences. This makes it harder to interpret directly. On the other hand as already outlined above, standard deviation is simply the square root of variance. This step brings the measure back into the original units of the data, for example returns measured as a percentage, which makes it more intuitive and practical.

How is Standard Deviation Related to the Sharpe Ratio?

Standard deviation is key in calculating the Sharpe ratio, which is a widely popular measure of risk-adjusted returns. It evaluates how much excess return an investment generates per unit of risk. It is calculated as:

Where:

Rp = portfolio return

Rf = risk-free rate

p = standard deviation of portfolio returns

A lower standard deviation means returns were achieved using a lower level of risk and a higher Sharpe ratio respectively (assuming returns stay constant). Conversely, higher volatility could lead to a lower Sharpe ratio, signalling poorer risk-adjusted performance.

Conclusion

Overall, deviation risk measures are practical tools for assessing the variability of investment returns. They find many applications in portfolio management and analysis, but since they assume normal distribution of returns are unable to fully capture asymmetric risks or extreme tail events. Therefore, when used alongside spectral risk measures such as Conditional Value at Risk (CVaR), deviation measures contribute to a more rounded and complete risk assessment.

Additional Resources

Portfolio Analysis

Portfolio Construction

Portfolio Management Certification